Mesures, graphiques, modélisation et incertitudes

Introduction

Les graphiques sont très utilisés en sciences, en histoire ou en commerce car ils permettent de rendre compte visuellement de l’évolution d’un ensemble de données, généralement regroupé dans un tableau qui, lui, est peu lisible.

A voir dans ce cours

Autre cours à consulter

Capacités et compétences travaillées

Consignez les mesures dans un tableau

Avant de construire un graphique, les données mesurées doivent être rassemblées dans un tableau de mesure.

Prenons l’exemple d’une expérience au cours de laquelle nous mesurons la température (T) d’une eau au cours du temps (t), ou la durée Δt. L’ensemble des mesures peut être présentées sous forme d’un … :

Tableau de mesure horizontal

Il faut présenter ainsi lors de la rédaction de vos comptes rendus de travaux pratiques.

Tableau de mesure vertical

Éviter de présenter ainsi. Pas faux mais cela prendrait trop de place sur vos copies.

Les tableurs Excel, LatisPro ou Calc. présentent leurs tableaux de données ainsi et s’enregistrent sous formats *.csv, *.json.

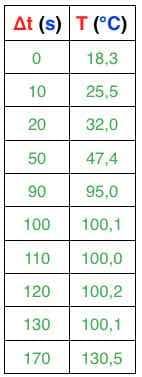
En physique chimie, les entrées d’un tableau correspondent aux grandeurs physiques avec leur unité de mesure.

Dans le domaine du bigdata, les entrées des tableaux sont appelées descripteurs.

Travail à faire n° 1 :

Construisez le graphique de l’évolution de la température T en fonction de la durée Δt de l’expérience.

Si vous éprouvez des difficultés à construire ce graphique, consultez le diaporama ci-dessous pour vous aider pas-à-pas.

Une solution est proposée un peu plus bas.

Le graphique

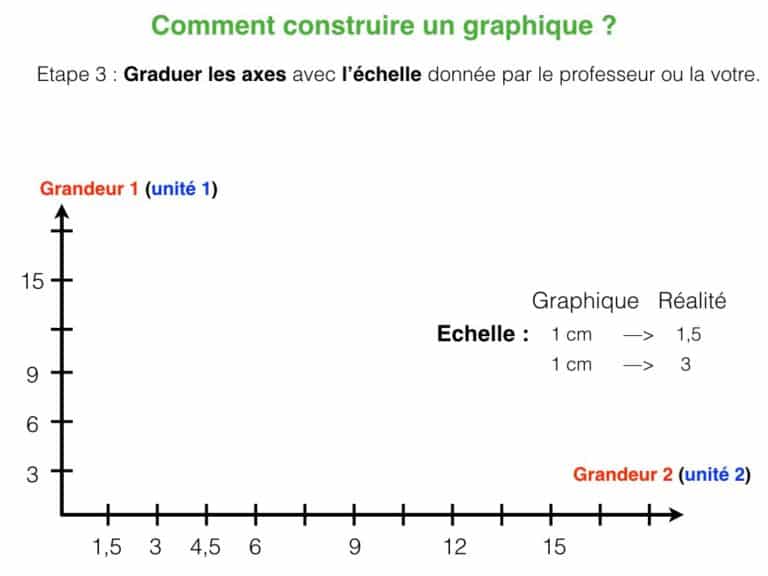
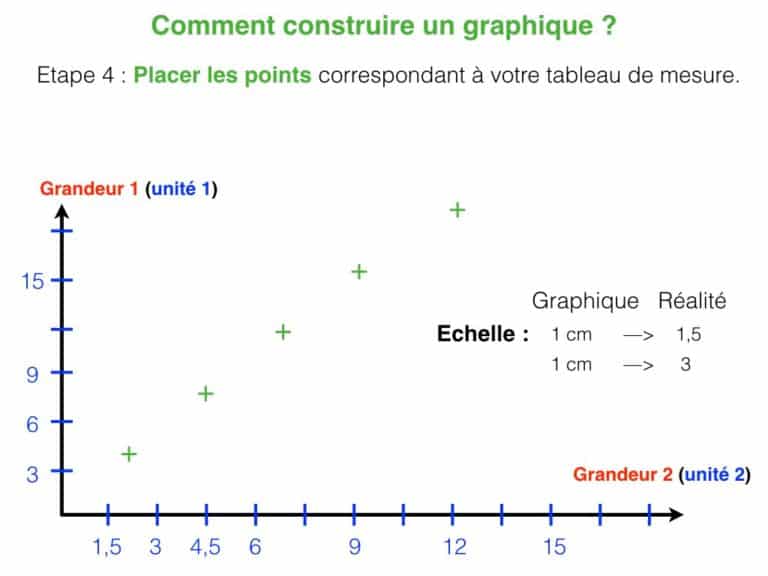
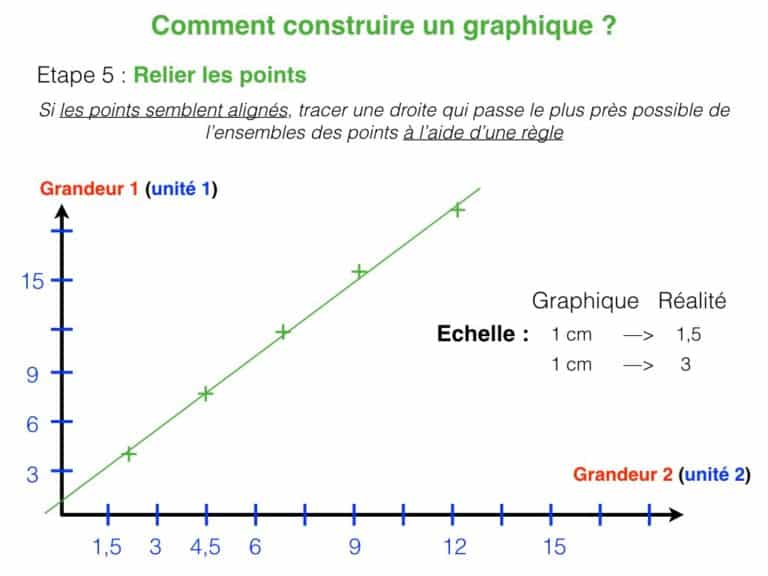
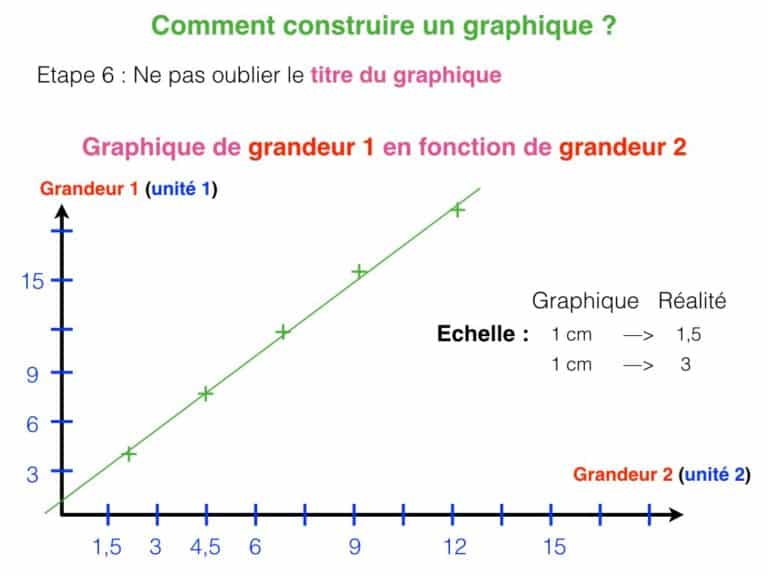
Concernant le travail précédent, voici une solution :

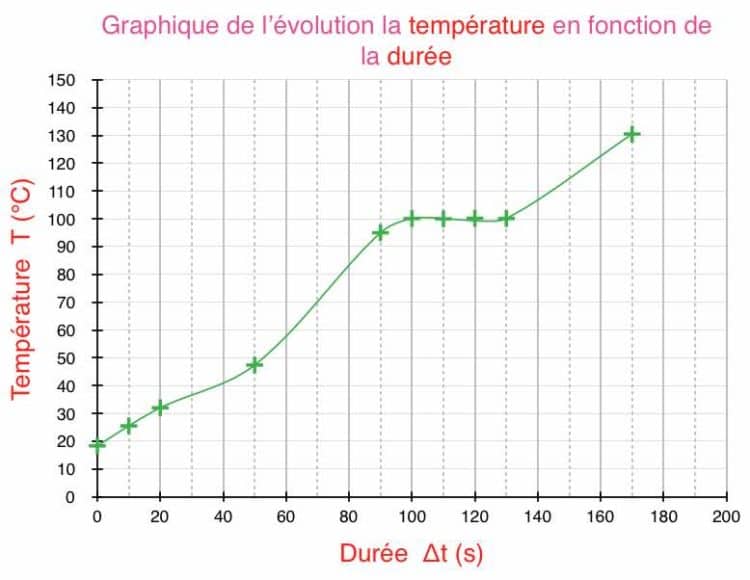
Modélisation d'une série de mesure

Les différentes équations rencontrées en physique chimie

Vous avez vu en mathématique que toutes droites ou courbes d’un graphique peuvent être représentées par une fonction : y = f(x).

En seconde et première

On modélisera tout le temps les graphiques par une droite affine :

y = a•x + b

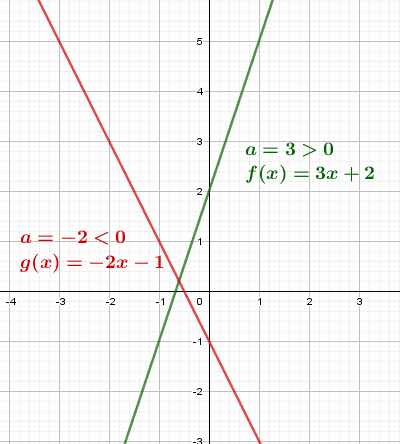
En terminale

On modélisera soit par un droite affine soit par une équation du seconde degré :

y = a•x² + b•x +c

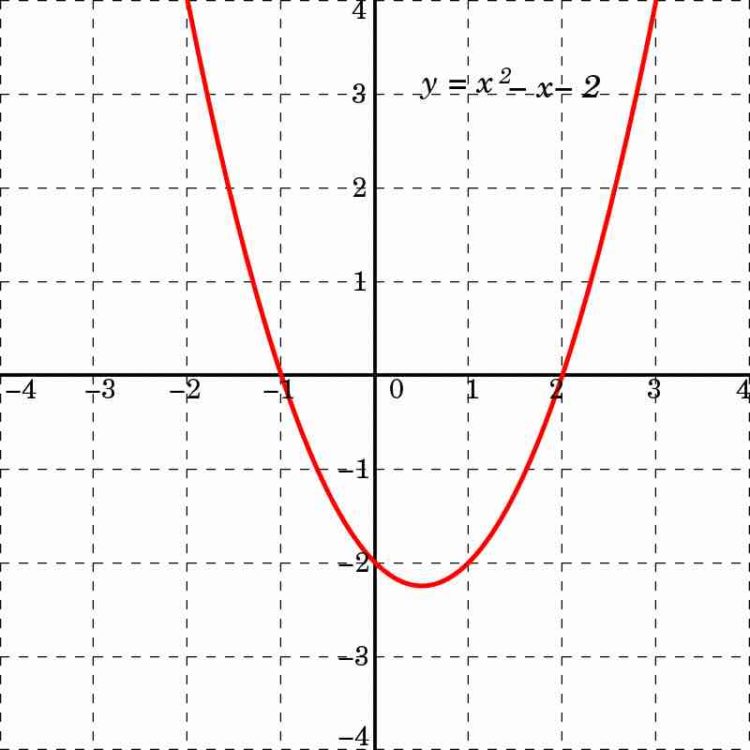
Droite affine

Cette animation vous montre comment on détermine un coefficient directeur et une ordonnée à l’origine pour une droite. Des jeux / exercices sont proposés pour tester vos connaissances.

Comment utiliser sa calculatrice pour modéliser une série de mesure ?

Pour obtenir le tutoriel, cliquer sur votre calculatrice ci-dessous et rendez vous page 1 : Représentation graphique. (Source : math.univ-lyon1.fr)

TI 83 Premium

Casio Graph

TI 82 Advanced

TI 83

TI 89 Titanium

TI nspire

Exemple de modélisation d'une série de mesure

Travail à faire n° 2 :

Une élève décide de tester la loi d’Ohm qui nous dit : « la tension U aux bornes d’un conducteur ohmique est proportionnelle à l’intensité I qui le traverse ». Sa série de mesure est consignée dans le tableau ci-dessous :

A l’aide de votre calculatrice (voir les tuto ci-dessus) ou du logiciel LatisPro, tracer le graphique U = f(I).
Modéliser la courbe et écrire l’équation de la droite modèle (voir correction ci-dessous)
On sait que u(U) = 0,2 V et u(I) = 0,1 A. Avec votre calculatrice ou LatisPro, déterminer la résistance R_exp et son incertitude-type u(R).

Correction :

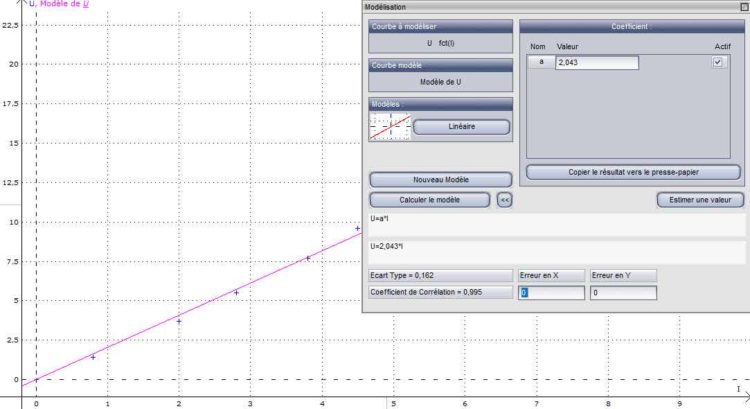
2/ Modélisation de U = f (I) à l’aide du logiciel Latis Pro

L’équation de la droite affine modèle (y = a⋅x ) est U = a⋅I avec a = R_exp = 2,043 Ω = 2,0 Ω (en tenant compte des chiffres significatifs)

Le coefficient de corrélation est de 0,995 > 0,99. Le modèle choisi est donc pertinent.

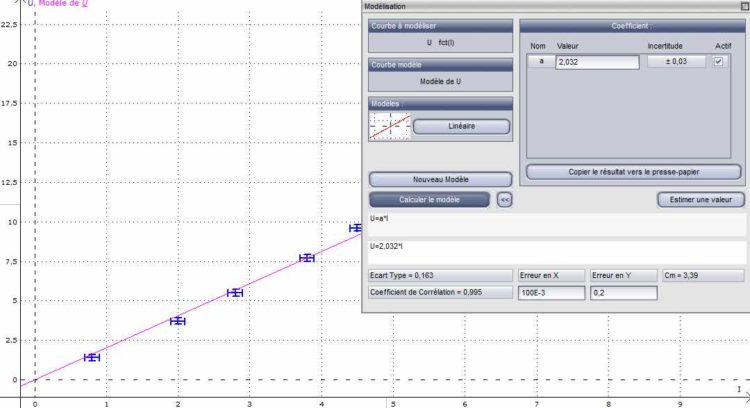
3/ Estimation de l’incertitude-type sur la détermination de a = R_exp.

L’équation de la droite est toujours la même mais nous avons maintenant accès à l’incertitude type u(a) du coefficient directeur qui correspond à la valeur expérimentale de la résistance du conducteur ohmique : u(R) = u(a) = 0,03 Ω

Nous devons arrondir au supérieur en respectant les chiffres significatifs : u(R) = 0,1 Ω

R_exp = (2,0 ± 0,1) Ω

Ajustement des courbes

Cette animation vous permet de placer les points où vous le souhaitez puis vous pourrez choisir / tracer la droite ou courbe qui modélise le mieux vos mesures.