Tous les instruments de mesure présentent une incertitude, un intervalle de confiance de la mesure. Ainsi, une même balance peut afficher 3 ou 4 mesures différentes pour un même objet …
Mais alors, les instruments de mesures sont-ils fiables ? Pourquoi la science moderne s’appuie-elle malgré tout sur les mesures pour expliquer le monde ?
Les scientifiques disposent d’outils mathématiques et de protocoles pour s’affranchir de ses incertitudes de mesures et présenter des conclusions fiables.
A voir dans ce cours
Autre cours à voir
Capacités et compétences travaillées
- Collecter des données
- Effectuer des calculs
- Utiliser l'écriture littérale
- Ecrire le bon nombre de chiffres significatifs
Consignez les mesures : le tableau
Les données mesurées sont rassemblées dans un tableau.
En guise d’exemple, sont consignées ci-dessous les mesures de masse d’un volume d’eau de 20 mL. L’ensemble des résultats doit être présentés sous la forme d’un tableau horizontal lors de la rédaction des comptes rendus de travaux pratiques.
En physique chimie, les entrées d’un tableau correspondent à des grandeurs physiques avec leur unité de mesure.
L'histogramme et le calcul de la moyenne (seconde)
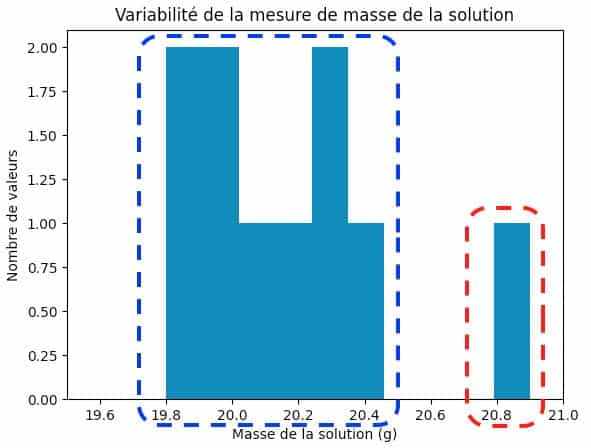
L’histogramme est un outil très utile pour se rendre compte en un coup d’oeil de la disparité des mesures. Elle permet aussi de voir les erreurs :
- Systémiques : Instruments mal calibrés, protocole mal rédigé.
- La négligence : Nul n’est parfait…
Histogramme
Remarques
La mesure 20,9 g est une erreur systémique ou de négligence car trop éloignée des autres. Nous l’enlèverons pour la suite.
Les autres mesures sont regroupées : nous calculerons alors une moyenne avec ces mesures-là.
Travail n°1 : Calculer la moyenne de l’ensemble des mesures en utilisant la formule suivante :
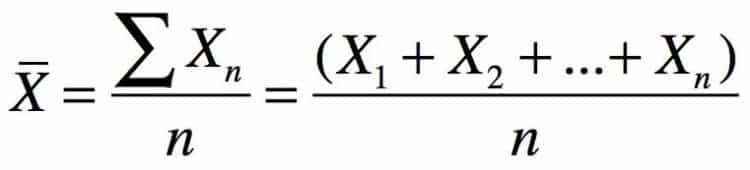
Correction :
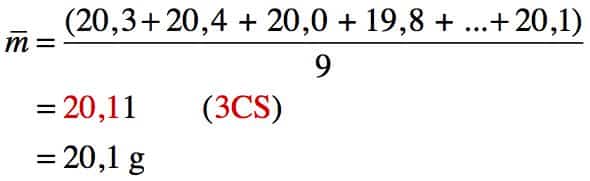
Calculs statistiques : incertitude de type A (Terminale)
On estime les incertitudes de type A lorsque l’expérimentateur dispose d’un échantillon de N valeurs mesurées … :
- avec le même opérateur, le même instrument de mesure, le même protocole: rigoureux
- avec des opérateurs différents, des instruments de mesure différents, le même protocole : moins rigoureux
Présentation des calculs statistiques
X = X̄ ± u(X)
- Moyennes, notées X̄
- Ecart-types, notées s(X)
- Incertitudes-types, notées u(X) (niveau de confiance de 68 %) :
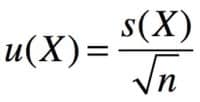
Les formules sont à disposition à la fin de votre livre de cours mais le plus simple est d’utiliser votre calculatrice pour ces opérations fastidieuses.
Comment utiliser sa calculatrice pour estimer une incertitude-type ?
Pour obtenir le tutoriel, cliquer sur votre calculatrice ci-dessous et rendez vous page 2 : Compléments : Données brutes (sans effectif)
(Source : math.univ-lyon1.fr )
TI 83 Premium
Casio Graph
Numworks
TI 82 Advanced
TI 83
TI 89 Titanium
TI nspire
Confrontation d'une valeur expérimentale avec une valeur théorique
On calculera le z-score :
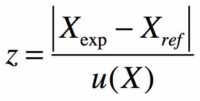
- Si z est inférieur à 2, plus la mesure Xexp est jugée compatible avec la valeur de référence Xref.
- Si z est supérieur à 2, soit il y a eu une erreur de manipulation ou de calcul, soit nous avons sous-estimé l’incertitude.
Remarque : Post bac, vous n’utiliserez plus le z-score mais les incertitudes élargies, notées U(X) (différent de u(X)) dont le calcul est, pour avoir un niveau de confiance à 95 % : 
Exemple de calculs statistiques
Travail n° 2 : Estimons l’incertitude-type des mesures du travail n°1.
En insérant les mesures de masse du travail précédent dans la calculatrice, on obtient les valeurs ci-dessous :
La calculatrice nous donne directement accès à :
- La moyenne des masses : m̄ = 20,1111 = 20,1 g
- L’écart-type : s(m) = 0,202759 g
- Le nombre de mesure : n = 9
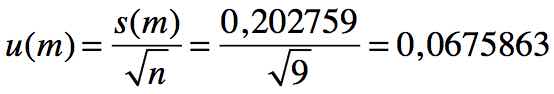
Vu le résultat de la moyenne et notre calcule d’incertitude type, on ne garde qu’un seul chiffre significatif : u(m) = 0,1 g (ne pas oublier l’unité)
Présentation du résultat : m = (20,1 ± 0,1) g
Confiance à 68 % (k=1)
On utilise l’incertitude type u(m)
m = 20,1 ± k × 0,1
m = (20,1 ± 0,1) g
Confiance à 95 % (k=2)
On utilise l’incertitude élargie U(m)
m = 20,1 ± k × 0,1
m = (20,1 ± 0,2) g
Confiance à 99 % (k=3)
m = 20,1 ± k × 0,1
m = (20,1 ± 0,3) g