Ondes, diffraction et interférences
Cette animation vous permettra de simuler des expériences de diffraction ou d’interférences avec des ondes sonores, lumineuses ou mécaniques.
Autres cours à consulter
Liste des travaux pratiques (TP) au lycée sur les ondes sonores
Il existe plusieurs types de lumières
Les domaines des ondes lumineuses
Cette animation vous permettra de visualiser les différents domaines (IR, UV, RX…), en fréquence et en longueurs d’onde, de la lumière (ou onde électromagnétique). Une présentation des applications dans la vie de tous les jours est aussi proposées pour chaque domaine.
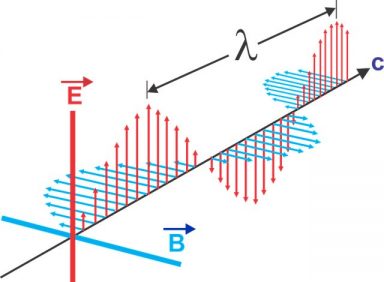
La lumière possède donc différents visages. Toutes ces lumières sont de même nature : une onde électromagnétique qui se propage comme une onde à la surface de l’eau ou une ola dans un stade. Les expériences suivantes prouvent que la lumière peut être considérée comme une onde.
Expériences de diffraction et d'interférences
Expériences
Cette vidéo montre des expériences de diffraction et d’interférences lumineuses avec la présentation du matériel adéquat.
Source – chaine Youtube : « TSG physics »
Modèle schématique des expériences de diffraction et interférences
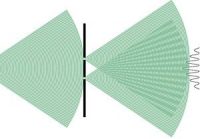

Diffraction et interférences
TP diffraction et interférence d'une onde lumineuse ou sonore
Je vous invite à consulter la simulation et le travail se trouvant sur les pages web suivante :
Source – phychiers.fr & Phetcolorado.edu



