Ce travail pratique sur l’étude de l’écoulement des fluides, théorisé par M. Bernoulli, permet de comprendre le réseaux sanguins de l’Homme, d’expliquer l’effet Venturi que l’on peut constater lors de vents violents entre 2 immeubles.
Débit volumique
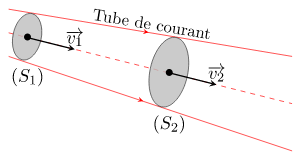
Relation de Bernoulli
P : La pression du fluide (en Pascal Pa)
v : La vitesse d’écoulement du fluide (en m/s)
g : L’intensité de pesanteur de la Terre (N/kg)
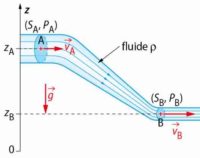
La relation de Bernoulli nous dit que les grandeurs mesurables en un point A d’un fluide (ici, de l’eau) sont liées à celle du point B. La relation de Bernoulli s’écrit alors :

Capacités et compétences travaillées
- Collecter des données
- Effectuer des calculs
- Utiliser l'écriture littérale
- Ecrire le bon nombre de chiffres significatifs
- Comparer à une valeur de référence
A l’aide de la simulation d’expérience « Flux et fluide » ci-dessous, réalisez le travail demandé sous l’animation.
Les différentes ondes
Cette animation vous permettra de visualiser différents fluides s’écoulant dans une canalisation et de mesurer, en différents points, les vitesses, les pressions en différents points.
Si vous n’arrivez pas visualiser l’animation ci-dessous, changer de navigateur (Chrome, Edge, Mozilla)
Paramètres à rentrer :
- Sélectionner le « flux » sur l’animation ci-dessus.
- L’animation modélise la canalisation d’un pipeline qui achemine du gasoil entre les pays.
- Rétrécissez la canalisation en son milieu à l’aide d’une des poignées.
- On fera s’écouler du gasoil dans la canalisation : dans le cadre jaune en bas à droite, bouger le curseur sur « gasoil ».
- Aux points A, B et C … :
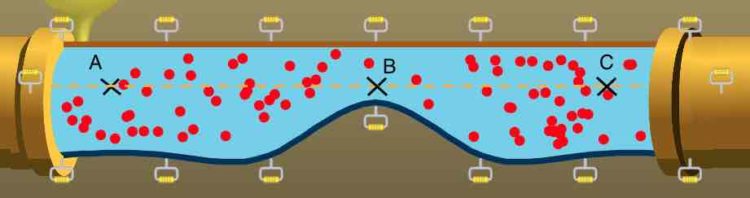
Les mesures se feront à la même altitude pour pouvoir simplifier la relation de Bernoulli par la suite.
Etude de l’écoulement permanent d’un fluide pour tester la relation de Bernoulli
Travail : L’effet venturi
- Si cela n’a pas encore été fait, ouvrez et entrez les paramètres de l’animation décris au-dessus.
- Mesurer la pression du fluide, la vitesse d’écoulement du fluide, la masse volumique du fluide et l’intensité de pesanteur de la Terre à ces 3 points.
- Vérifier que la relation de Bernoulli (voir ci-dessus) est constante en chaque point.
- Lorsque la canalisation se rétrécit, décris comment évolue la vitesse et la pression du fluide… c’est l’effet Venturi.
Exploitation de la conservation du débit volumique
Travail :
- Si cela n’a pas encore été fait, ouvrez et entrez les paramètres décris sous l’animation.
- Mesurer les vitesses vA, vB et vC aux points A, B et C à l’aide du tachymètre.
- Mesurer le diamètre de la section du pipeline aux points A, B et C à l’aide de la règle. En déduire la surface S de la section du tuyau.
- A l’aide de vos résultats des questions précédentes, calculer le débit volumique aux points A, B et C.
- Comparer avec la valeur affichée par l’animation en haut à gauche. Commenter.


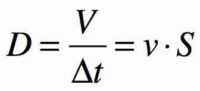
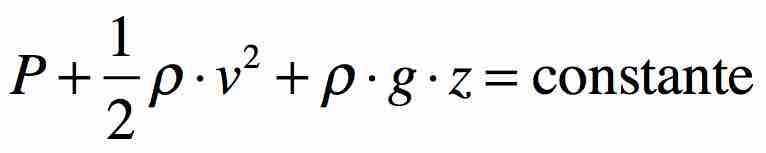
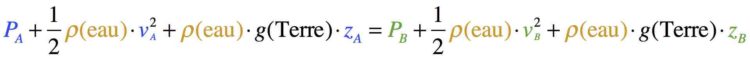
comment calculer la constante de bernouilli sans z ?
Bonjour Romi. Il n’existe pas de constante de Bernoulli. Par contre il y un principe de Bernoulli.